非监督学习

在一组数据中寻找某种结构或模式

关联规则挖掘

关联规则挖掘可以从数据集中发现项与项（item 与item）之间的关系

支持度

指一组频繁模式的出现概率，表示项集{X,Y}在总项集里出现的概率。表示A和B同时在总数I 中发生的概率

$$ Support(X,Y) = P(XY) = \frac{number(X,Y)}{number(总样本)} $$

置信度

衡量频繁模式内部的关联关系，体现了一个数据出现后，另一个数据出现的概率

$$ Confidence(X ⇐ Y) = P(X|Y) = \frac{P(X|Y)}{P(Y)} $$

提升度

表示含有X的条件下，同时含有Y的概率，与只看Y发生的概率之比。提升度反映了关联规则中的X与Y的相关性，提升度>1且越高表明正相关性越高，提升度<1且越低表明负相关性越高，提升度=1表明没有相关性，即相互独立

$$ Lift(X → Y) = \frac{P(Y|X)}{P(Y)} $$

Apriori 算法

算法流程

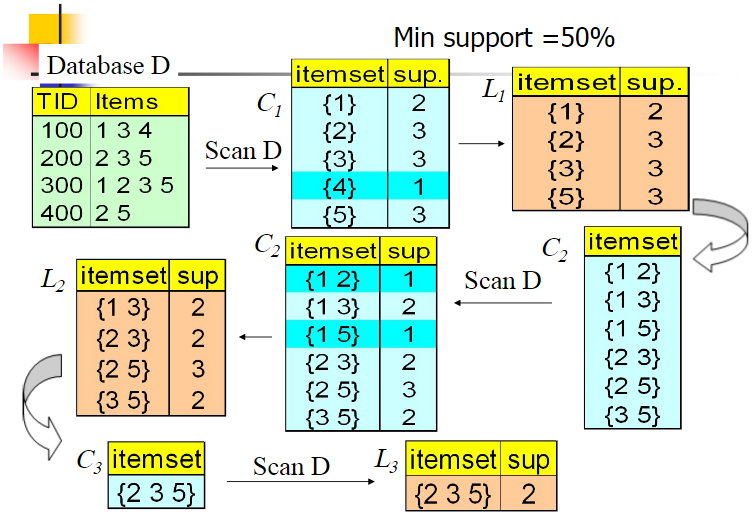
如果 123 是频繁组合，则 12、13、23 也是频繁组合；若 12 是非频繁组合，则 123 也是非频繁组合

FP-Growth 算法

创建了一棵 FP 树来存储频繁项集。在创建前对不满足最小支持度的项进行删除，减少了存储空间，整个生成过程只遍历数据集 2 次

聚类

根据形成聚类方式的不同，聚类算法可以分为：

层次聚类：以一种层次化的方式组织数据，逐步合并或分裂聚类，形成一个层次结构。可以是自下而上（凝聚性聚类）或自上而下（分裂性聚类）的方式
原型聚类：基于原型或中心点的概念，将数据划分为若干个类别。每个类别由其代表性的原型来描述，比如K均值聚类
分布聚类：假设数据符合某种概率分布，例如高斯混合模型（Gaussian Mixture Models，GMM）。试图拟合数据的分布，以确定聚类
密度聚类：考虑数据点的密度，将高密度区域视为一个聚类簇，并通过密度低的区域将聚类簇分隔开，比如DBSCAN算法

分级聚类

不断将最为相似的群组两两合并

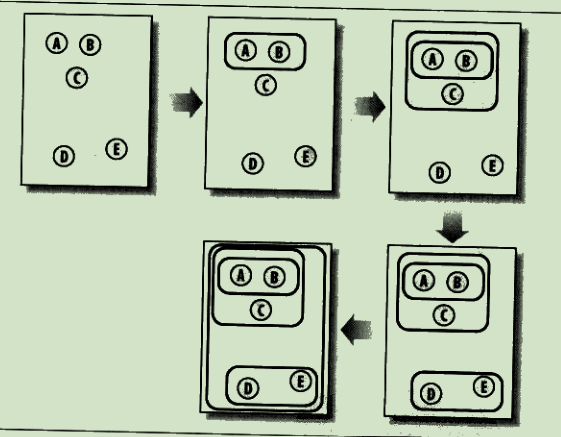
屏幕截图 2020-10-13 103115

使用树状图来可视化聚类结果，通过路径长度来体现各元素的相似度：

stateDiagram-v2
    direction LR
    cluster --> cluster1
    cluster1 --> cluster3
    cluster3 --> A
    cluster3 --> B
    cluster1 --> C
    cluster --> cluster2
    cluster2 --> D
    cluster2 --> E

K均值聚类

随机确定k个中心位置
将各个数据项分配个最近的中心点
将中心点移动到各个节点的平均位置
重复2-3 直到不再变化

如果某个点比较倒霉，初始被分配到的地方找不到与其最近的点，那一般就会把这个聚类去掉，变成 K - 1 个聚类

所以，代价函数是

$$ J =\frac{1}{m}\sum_{i=1}^{m}|x^{(i)}-\mu_{c^{(i)}}|^{2} $$

如果代价函数值增加了，一定是实现出了问题

选择初始点：

K要小于训练数据数量
随机从训练数据中挑选 K 个点作为初始点
这种随机初始化有可能找到的是局部最优解，所以需要多轮随机选择，选择代价函数最小的初始点

选择K：

一种办法是尝试不同的K，使用代价函数较小，K也合适的，这会导致算法偏向于更大的K
另外一种选择K的办法是K应该是要跟解决的问题相关，要根据业务来决定

EM聚类

stateDiagram-v2
    初始化参数 --> 观察预期: Exception
    观察预期 --> 重新估计参数: Maximization
    重新估计参数 --> 初始化参数

EM 算法相当于一个框架，可以采用不同的模型来进行聚类，比如 GMM（高斯混合模型），或者 HMM（隐马尔科夫模型）来进行聚类

异常检测

给定数据集 X，我们假使数据集是正常的，我们希望知道新的数据是不是异常的，即这个测试数据不属于X的几率如何

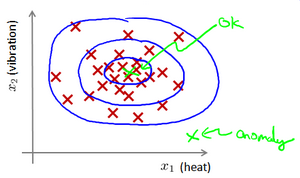
蓝色圈内的数据属于该组数据的可能性较高，越是偏远的数据，其属于该组数据的可能性就越低

这种方法称为密度估计

$$ if\quad p(x)\begin{cases}<\varepsilon&anomaly\>=\varepsilon&normal&\end{cases} $$

可以用高斯分布来确定已知$x^{(i)}$，求其概率：

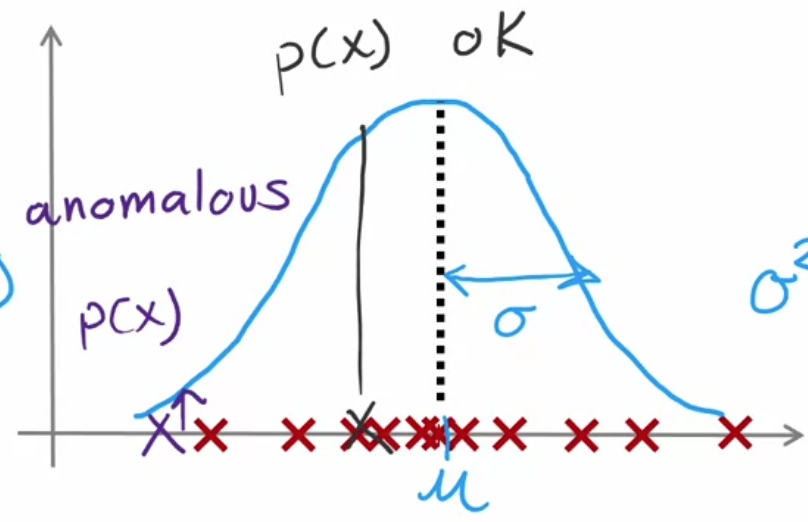
高斯分布（正态分布）

高斯分布由两个参数计算确定：

$$ \mu=\frac1m\sum_{i=1}^mx^{(i)}\ \sigma^2=\frac1m\sum_{i=1}^m(x^{(i)}-\mu)^2 $$

计算一个特征向量出现的概率：

$$ p(\vec{\mathrm{x}})=p(x_1;\mu_1,\sigma_1^2)p(x_2;\mu_2,\sigma_2^2)p(x_3;\mu_3,\sigma_3^2)\cdotsp(x_n;\mu_n,\sigma_n^2)\ =\prod_{j=1}^np(x_j;\mu_j,\sigma_j^2) $$

每一个特征都需要计算自己的高斯分布，即自己的$\mu$ $\sigma^2$：

$$ \mu_{j}=\frac{1}{m}\sum_{i=1}^{m}x_{j}^{(i)}\ \sigma_{j}^{2}=\frac{1}{m}\sum_{i=1}^{m}(x_{j}^{(i)}-\mu_{j})^{2} $$

由于异常检测是无监督学习，所以是通过训练集构建密度估计函数，再通过验证集（大量正常数据，少量异常数据）选择合适的$\epsilon$

对比项	异常检测	监督学习
训练数据特征	非常少量的正向类（异常数据 y = 1）, 大量的负向类（y = 0）	同时有大量的正向类和负向类
正向数据占比	许多不同种类的异常，非常难。根据非常少量的异常数据来训练算法。	有足够多的正向类实例，足够用于训练算法，未来遇到的正向类实例可能与训练集中的非常近似。
挖掘模式	未来遇到的异常可能与已掌握的异常、非常的不同。	找出已存在于训练数据中的模式
场景	欺诈行为检测生产（例如飞机引擎）检测数据中心的计算机运行状况	邮件过滤器天气预报肿瘤分类

异常检测假设特征符合高斯分布，如果数据的分布不是高斯分布，异常检测算法也能够工作，但是最好还是将数据转换成高斯分布，例如使用对数函数 $x = log(x + c)$ 或者 $x = x^c$

我们通常可以通过将一些相关的特征进行组合，来获得一些新的更好的特征（异常数据的该特征值异常地大或小