数据的表示
组织数据,方便计算机硬件直接使用
机器内的数据表示
原码
原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小
反码
反码跟原码是正数时,一样;负数时,反码就是原码符号位除外,其他位按位取反
补码
仍然通过最左侧第一位的 0 和 1,来判断这个数的正负。但是,不再把这一位当成单独的符号位,在剩下几位计算出的十进制前加上正负号,而是在计算整个二进制值的时候,在左侧最高位前面加个负号
1000 表示 -8,0010 代表 2
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理
移码
对补码的符号位取反
定点与浮点数据表示
定点数
- 可表示定点小数和整数
一个 32 比特的可以代表8个 0 ~ 9的整数,最右边的 2 个 0~9 的整数,当成小数部分;把左边 6 个 0~9 的整数,当成整数部分
用二进制来表示十进制的编码方式,叫作BCD编码
这种方式有两个缺点:
- 表示的数值范围较小
- 没办法同时表示很大的数字和很小的数字
浮点数

- S是一个符号位,用来表示是正数还是负数
- 偏指数E,用来表示2的e次方的取值空间
- 尾数位数,代表有效数位
不同系统可能根据自己的浮点数格式从中提取不同位数的阶码
- IEEE 754格式
| S | 8位偏指数E | 23位有效尾数M | 单精度 |
|---|---|---|---|
| S | 11位偏指数E | 52位有效尾数M | 双精度 |
加法
两个浮点数的指数位可能是不一样的,在计算时要把两个的指数位变成一样的,然后只去计算有效位的加法,也就是把指数位都统一成两个其中较大的
两个相加数的指数位差的越大,位移的位数越大,可能丢失的精度也就越大
在实际计算的时候,只要两个数,差出 224,也就是差不多 1600 万倍,那这两个数相加之后,结果完全不会变化
- Kahan Summation的算法
在每次的计算过程中,都用一次减法,把当前加法计算中损失的精度记录下来,然后在后面的循环中,把这个精度损失放在要加的小数上,再做一次运算
for (int i = 0; i < 20000000; i++) {
float cur = 1.0f;
float needToAdd = cur + remain;
float nextRes = res + needToAdd;
remain = needToAdd - (nextRes - res);
res = nextRes;
}
字符串的表示
字符编码 Character Encoding : 就是一套自然语言的字符与二进制数之间的对应规则。
- 字符集 Charset :也叫编码表。是一个系统支持的所有字符的集合,包括各国家文字、标点符号、图形符 号、数字等。
stateDiagram-v2
direction LR
GBK字节 --> GBK编码集
GBK编码集 --> 中文(你好)
中文(你好) --> GBK编码集
GBK编码集 --> GBK字节
UTF8字节 --> UTF8编码集
UTF8编码集 --> 中文(你好)
中文(你好) --> UTF8编码集
UTF8编码集 --> UTF8字节
常用编码
- ASCII 码 使用7bit来表示 范围从0-127
- ISO-8859-1 单字节编码 总共能表示256字符
- GB2312 双字节编码
- GBK 扩展了GB2312 增加了更多的汉字
- UTF-16 两个字节表示一个字符 大大简化了字符串操作 是Java内存的存储格式
- UTF-8 使用变长存储 不同的字符可以由1~6个字符组成
GBK与GB2312对比:GBK范围更大
UTF8与UTF16对比:16编码效率高 但不适合网络传输 8的容错性比16强
数据校验
受元器件的质量、电路故障或噪音干扰等因素的影响,数据 在被处理、传输、存储的过程中可能出现错误,若能设计硬件层面的错误检测机制,可以减少基于软件检错的代价
基本原理
- 增加冗余码
码距
- 同一编码中,任意两个合法编码之间不同二进数位数的最小值
- 校验码中增加冗余项的目的就是为了增大码距
- 码距≥e+1:可检测e个错误
- 码距≥2t+1:可纠正t个错误
- 码距≥e+t+1:可纠正t个错误,同时检测e个错误(e >= t)
奇偶校验
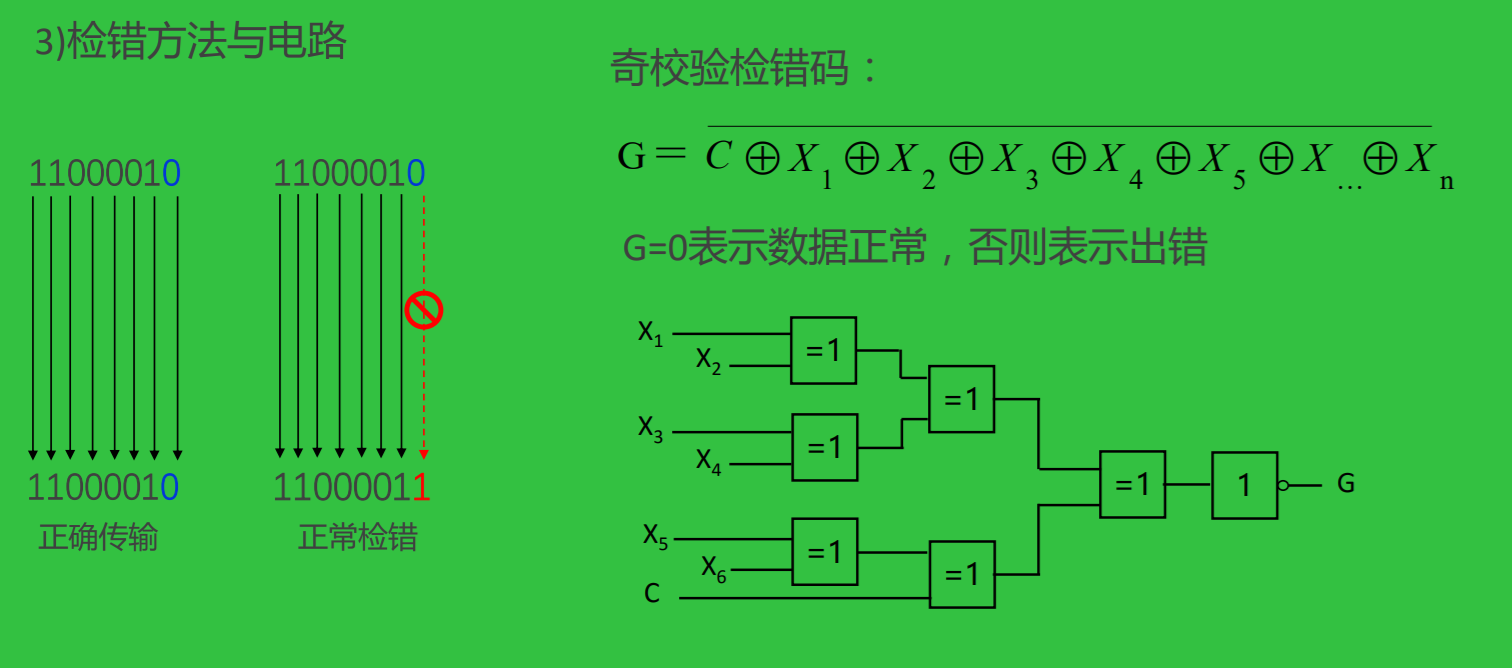
- 编码与检错简单
- 编码效率高
- 不能检测偶数位错误, 无错结论不可靠,是一种错误检测码
- 不能定位错误,因此不具备纠错能力
CRC校验
海明校验
海明码是采用奇偶校验的码,把这数据分了组,通过分组校验来确定哪一位出现了错误,原理
7-4海明码
一共是 7 位(Bit)有效数据并额外存储了 4 位数据,用来纠错
海明距离
对于两个二进制表示的数据,之间有差异的位数,称之为海明距离