堆
应用
- 优先级队列
堆的存储
二叉堆
- 是一棵完全二叉树
- 每个节点和其子节点都有一样的偏序关系,要么大于要么小于
大顶堆就要求堆中所有节点的值,一定大于其左右子树中的任何一个节点的值,小顶堆就正好相反
优先级队列适合用大顶堆实现,这样每次只需要从顶部取出元素即可获得优先级最高的元素
用数组存储二叉堆
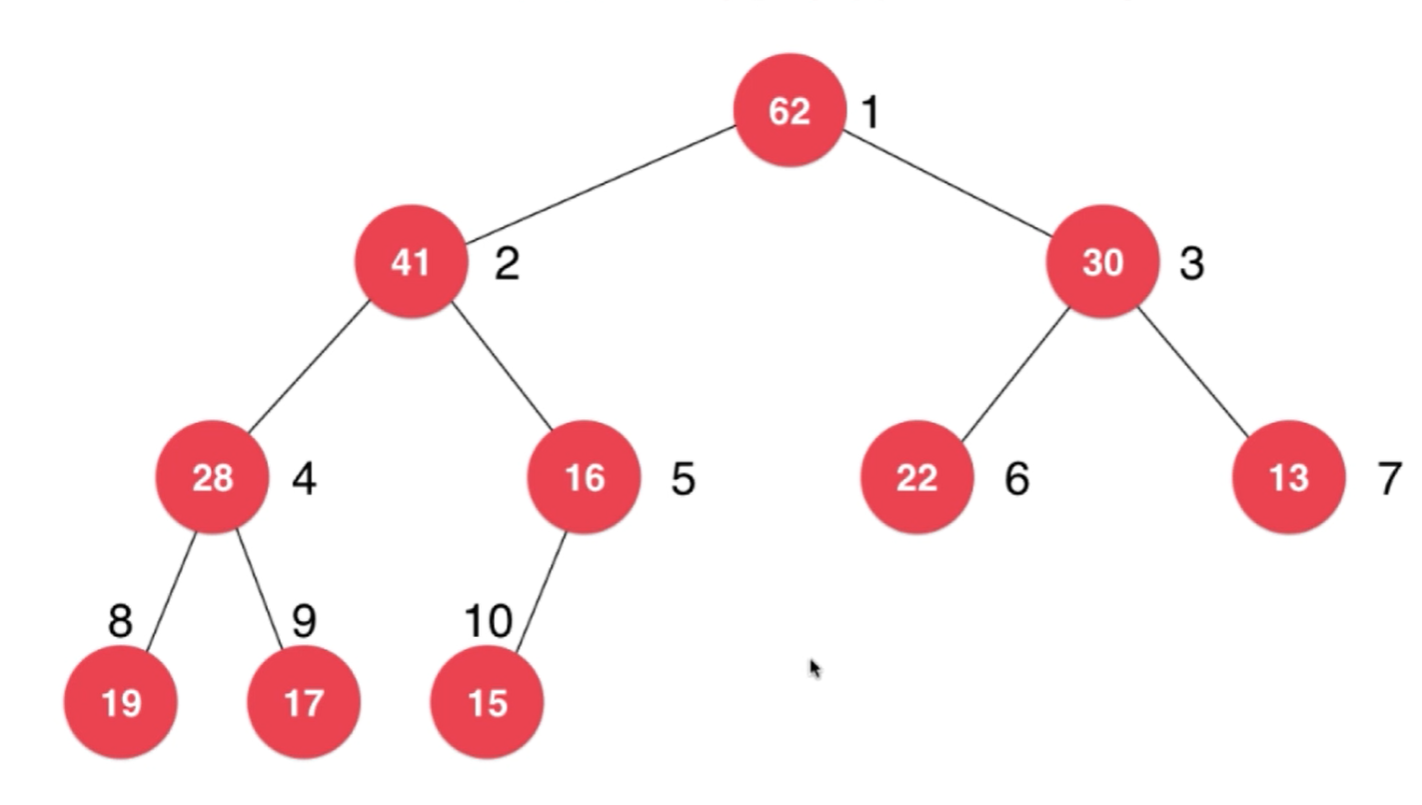
操作
- sift up
新加入的元素与其父元素判断,是否比父元素大,如果是,交换两个元素,以此类推,直到小于其父亲
while (less(data,i/2,i)) {
swap(data,i/2,i);
i/=2;
}
- sift down
只能取出根节点的元素,取出后,使用堆中的最后一个元素填补空缺
填补后,跟左右两个孩子比较,哪个孩子大就跟谁交换...以此类推,直至自己比两个孩子都大
while (2 * k <= count) {
int j =2*k;
// 确定要跟左子树比较还是跟右子树
if (j+1<=count && greater(data,j+1,j)){
// 右子树
j++;
}
// 如果自己大于要比较的子树,则停止
if (greaterThan(data,k,j)){
break;
}
swap(data,k,j);
k=j;
}
- 删除
将根节点删除后,我们把二叉堆中最后的元素提到根节点的位置,这样又可以保证新的二叉树是一颗满二叉树了,然后要做的比较 + 交换
堆排序
MaxHeap<Comparable<?>> heap = new MaxHeap<>(a.length+1);
for (int i = 0; i < a.length; i++) {
heap.insert(a[i]);
}
for (int i = 0; i < a.length; i++) {
a[i]=heap.remove();
}
Heapify(堆化【将数组转为堆】)
对于一棵完全二叉树,其最后一个非叶子节点是元素个数除二取整
所以要把一个数组堆化,只需要对其非叶子结点进行shift down
for (int i = 0; i < a.length; i++) {
data[i + 1] = a[i];
}
count = a.length;
// 对其非叶子结点进行shift down
for (int i = count / 2; i >= 1; i--) {
shiftDown(i);
}
原地堆排序
int n = a.length;
// 先将整个数组构造成一个最大堆
for (int i = (n - 2) / 2; i >= 0; i--) {
shiftDown(a, n, i);
}
// 将堆中的第一大元素移到末尾,再次构造最大堆(排除末尾排好序的元素)
// 然后下一次循环再将第一大元素移到倒数第二个...以此类推,直至只剩一个元素
for (int i = n - 1; i > 0; i--) {
swap(a, 0, i);
shiftDown(a, i, 0);
}
索引堆
- 引入一个index数组,在增删改查的时候,提供一个index
- 索引堆根据这个index找到数据在data中的位置