字符串
排序
- 低位优先排序
public static void sort(String[]a,int W) {
int N = a.length;
int R = 256;
String[] aux = new String[N];
//循环W次键索引记数法
for(int d = W-1; d>=0;d--) {
int[] count = new int[R+1];
//键索引记数法第一步--频率统计
for(int i=0;i<N;i++)
count[a[i].charAt(d)+1]++;
//键索引记数法第二步--将频率转化为索引
for(int r=0;r<R;r++)
count[r+1]+=count[r];
//键索引记数法第三步--排序
for(int i=0;i<N;i++)
aux[count[a[i].charAt(d)]++] = a[i];
//键索引记数法第四步--回写
for(int i=0;i<N;i++)
a[i]=aux[i];
}
}
- 高位优先排序
public class MSD {
private static int R = 256; //字符串中最多可能出现的字符的数量
private static final int M = 15; //当子字符串长度小于M时,用直接插入排序
private static String[] aux; //辅助数组
//实现自己的chatAt()方法
private static int charAt(String s, int d) {
if(d<s.length())return s.charAt(d);
else return -1;
}
public static void sort(String[] a) {
int N = a.length;
aux = new String[N];
sort(a,0,N-1,0);
}
private static void sort(String[] a,int lo, int hi, int d) {
if(hi<=lo+M) {Insertion.sort(a,lo,hi,d);return;} //切换为直接插入排序
int[] count = new int[R+2];
//键索引记数法第一步
for(int i=lo; i<=hi;i++)
count[charAt(a[i],d)+2]++;
//键索引记数法第二步
for(int r=0;r<R+1;r++)
count[r+1]+=count[r];
//键索引记数法第三步
for(int i=lo;i<=hi;i++)
aux[count[a[i].charAt(d)+1]++] = a[i];
//键索引记数法第四步
for(int i=lo;i<=hi;i++)
a[i]=aux[i-lo];
//递归以每个字符为键进行排序
for(int r=0;r<R;r++)
sort(a,lo+count[r],lo+count[r+1]-1,d+1);
}
}
- 三向字符串快速排序
public class Quick3string {
private static int charAt(String s, int d) {
if(d<s.length())return s.charAt(d);
else return -1;
}
public static void sort(String[] a) { sort(a,0,a.length-1,0); }
public static void sort(String[] a,int lo, int hi, int d) {
if(hi<=lo) return;
int lt = lo, gt = hi;
int v = charAt(a[lo], d);
int i = lo+1;
while(i<=gt) {
int t = charAt(a[lo],d);
if(t<v) exch(a,lt++,i++);
else if(t>v) exch(a,i,gt--);
else i++;
}
sort(a,lo,lt-1,d);
if(v>=0) sort(a,lt,gt,d+1);
sort(a,gt+1,hi,d);
}
}
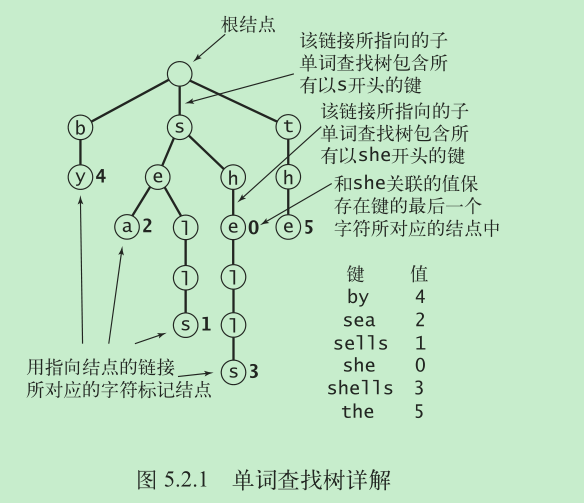
单词查找树
trie 树存储的开销要小得多,并且因为它天然的前缀匹配和排序的特性,在很多时候也能更快检索数据
stateDiagram-v2
g --> o
o --> l
l --> d
l --> a
a --> n
n --> s
查找
插入
查询所有键
- 通过递归的方式,如果有分叉,则生成一个由pre+branch的新字符串
public Interable<String> keys() {
return keysWithPrefix("");
}
public Interable<String> keysWithPrefix(String pre) {
Queue<String> q = new Queue<String>();
collect(get(root, pre, 0), pre, q);
return q;
}
private void collect(Node x, String pre, Queue<String> q) {
if (x == null) return;
if (x.val != null) q.enqueue(pre);
for (char c = 0; c < R; c++)
collect(x.next[c], pre + c, q);
}
- 删除
找到键所对应的结点并将它的值设为空(null)。如果该结点含有一个非空的链接指向某个子结点,那么就不需要在进行其他操作了。如果它的所有链接均为空,那就需要在数据结构中删去这个结点。如果删去它使得它的父结点的所有链接也均为空,就需要继续删除它的父结点,以此类推
public void delete(String key) {
root = delete (root, key, 0);
}
private Node delete(Node x, String key, int d) {
if (x == null) return null;
if (d == key.length())
x.val = null;
else {
char c = key.charAt(d);
x.next[c] = delete(x.next[c], key, d+1);
}
if (x.val != null) return x;
for (char c = 0; c < R; c++)
if (x.next[c] != null) return x;
return null;
}
三向单词查找树
在三向单词查找树(TST)中,每个结点都含有一个字符、三条链接和一个值。这三条链接分别对应着当前字母小于、等于和大于结点字母的所有键
子字符串查找
暴力查找
public static int search(String pat, String txt) {
int M = pat.length();
int N = txt.length();
// 逐个位置匹配模式字符串
for (int i = 0; i < N; i++) {
int j;
for (j = 0; j < M; j++) {
if (txt.charAt(i + j) != pat.charAt(j)) {
break;
}
}
// 找到了匹配的字符串
if (j == M) {
return i;
}
}
return N;
}
暴力查找(显式回退)
public static int searchother(String pat, String txt) {
int M = pat.length();
int N = txt.length();
int i;
int j;
// 逐个位置匹配模式字符串
for (i = 0, j = 0; i < N && j < M; i++) {
if (txt.charAt(i) == pat.charAt(j)) {
j++;
} else {
i -= j;
j = 0;
}
}
// 找到了匹配的字符串
if (j == M) {
return i - M;
} else {
return N;
}
}
KMP算法
根据模式构造一个DFA,使用DFA匹配
BM算法
跟KMP一样,都是通过对模式字符串进行预处理,从而加快搜索速度
坏字符
好后缀
RK指纹字符查找算法
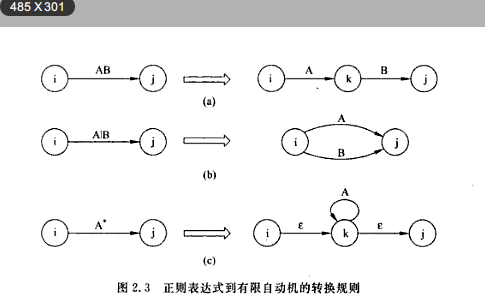
正则表达式
- 连接
AB -> {AB}
- 或
A|B -> {A,B}
- 闭包
B* -> 0个或多个B
构造正则表达式
数据压缩
游程编码
行程编码(Run Length Encoding,RLE), 又称游程编码、行程长度编码、变动长度编码 等,是一种统计编码。主要技术是检测重复的比特或字符序列,并用它们的出现次数取而代之
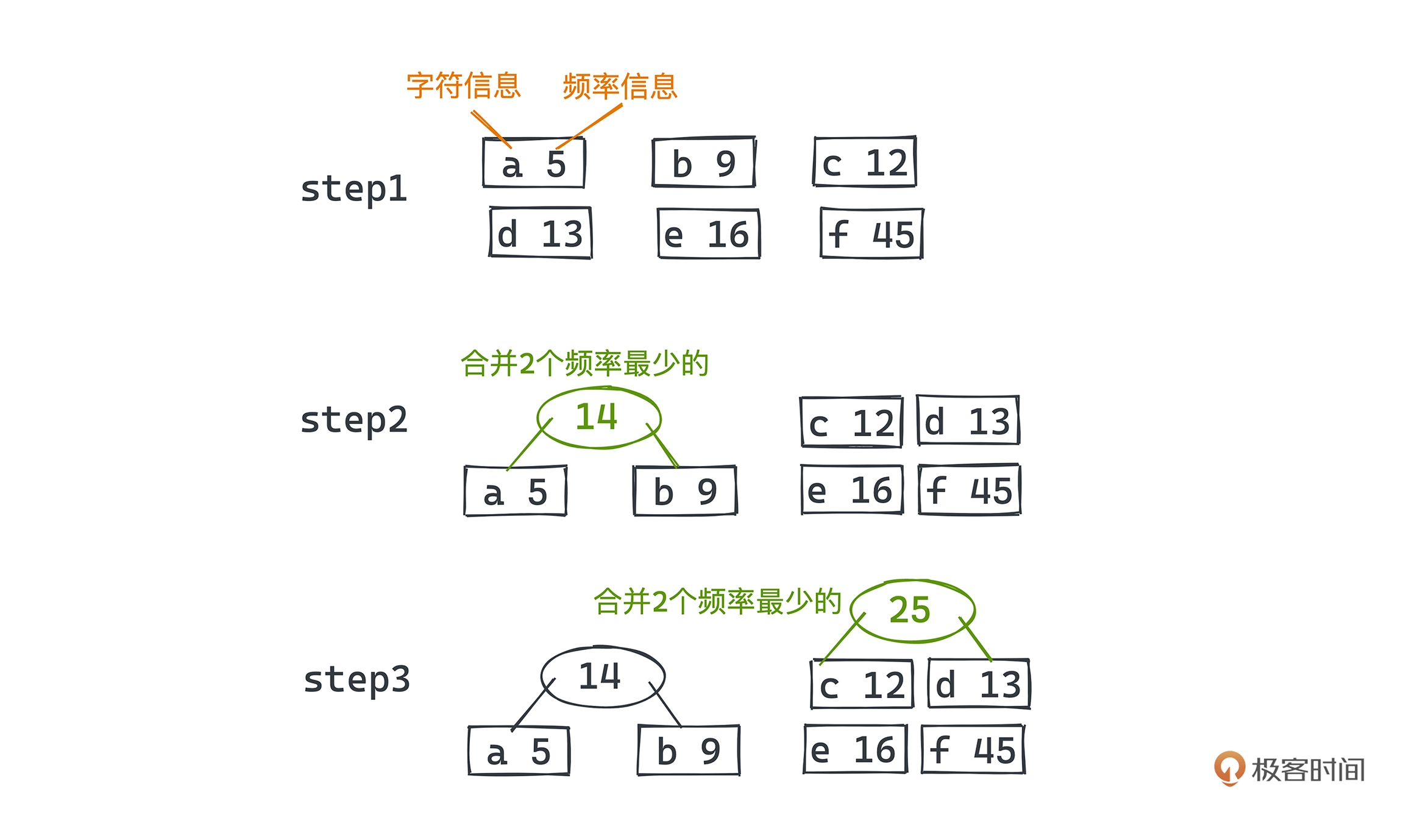
哈夫曼编码
用较少的比特表示出现次数多的字符,用较多的比特表示出现频率低的字符,不同的字符编码间不能彼此成为对方的前缀
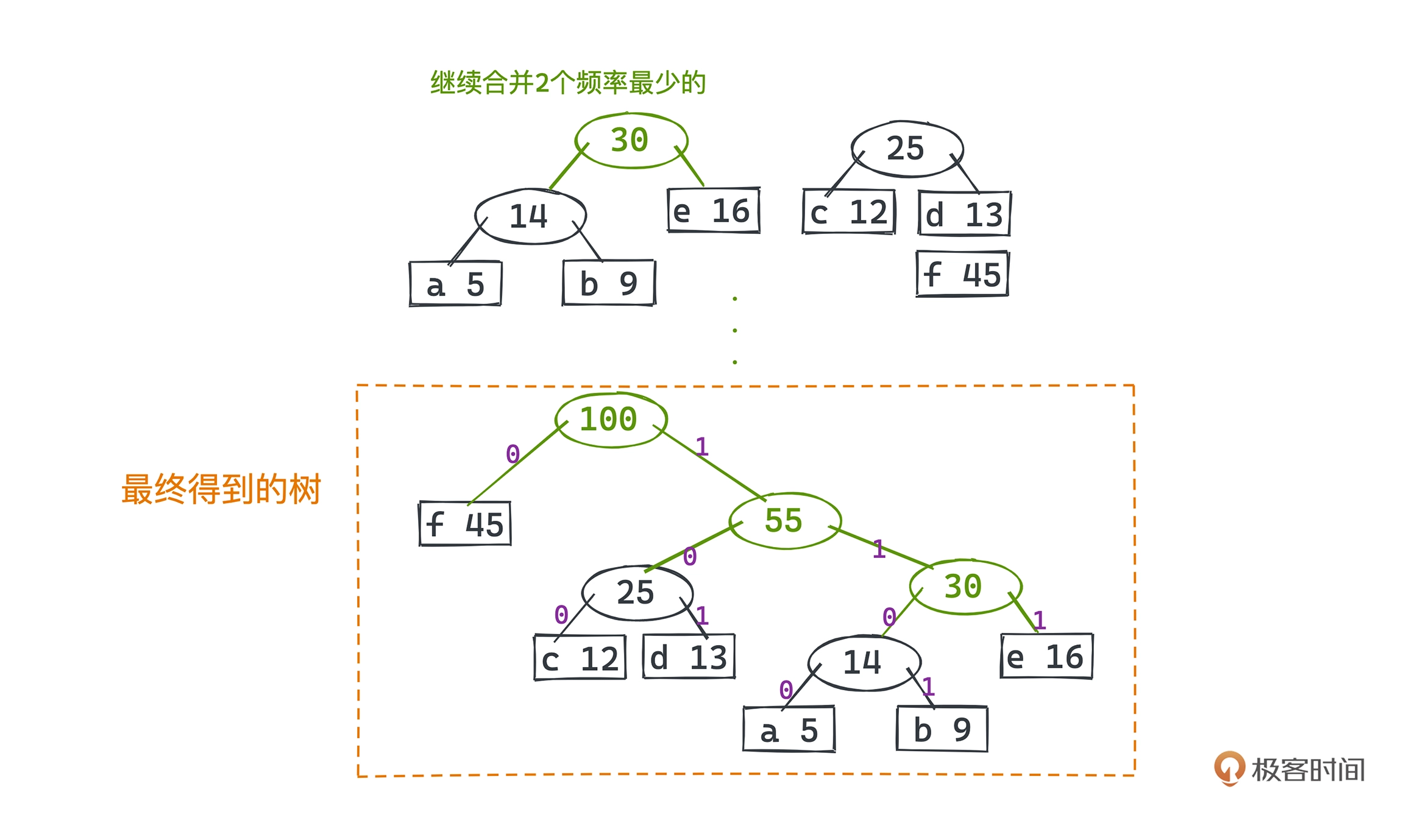
- 使用单词查找树实现
使用变长前缀,用一棵二叉树来标记每个字符的编码方式,左分支代表 0、右分支代表 1,所有需要编码的字符都对应二叉树的叶子节点,根结点到该叶子结点的路径就代表着该字符的编码方式
LZW压缩
LZW编码 (Encoding) 的核心思想其实比较简单,就是把出现过的字符串映射到记号上,这样就可能用较短的编码来表示长的字符串,实现压缩
LZW的一个核心思想,即压缩后的编码是自解释 (self-explaining) 的。什么意思?即字典是不会被写进压缩文件的,在解压缩的时候,一开始字典里除了默认的0->A和1->B之外并没有其它映射,2->AB是在解压缩的过程中一边加入的。这就要求压缩后的数据自己能告诉解码器,完整的字典,例如2->AB是如何生成的,在解码的过程中还原出编码时用的字典