排序
为什么要学习O(N^2)的排序算法
- 是其他算法的基础
- 编码简单
- 作为子过程,用于改进复杂的排序算法
排序算法的稳定性
对于相等的元素,在排序后,相对位置没有发生改变
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 直接选择排序 | O(n²) | O(n²) | O(n) | O(1) | 不稳定 |
| 直接插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(n²) | O(nlogn) | O(nlogn) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 希尔排序 | O(nlogn) | O(ns) | O(n) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(N*M) |
O(N*M) |
O(N*M) | O(M) | 稳定 |
选择排序
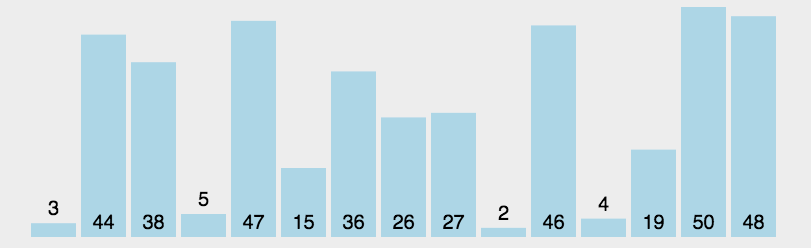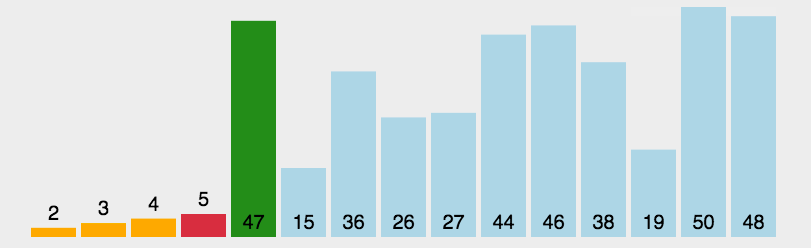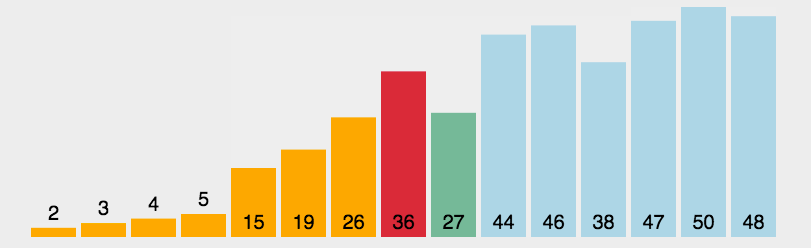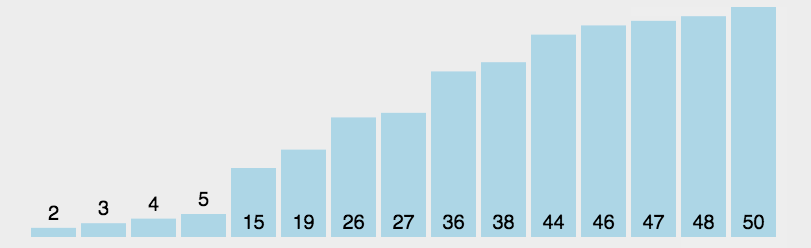
每一轮循环找到数组中最小的元素,第一次找到的最小元素将它与第一个元素交换位置,第二次找到的最小元素交换将它与第二个位置交换,以此类推
for (int i = 0; i < arr.length; i++) {
// 寻找[i,n)里的最小值
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (less(arr[j],arr[min])) {
min = j;
}
}
swap(arr, i, min);
}
插入排序
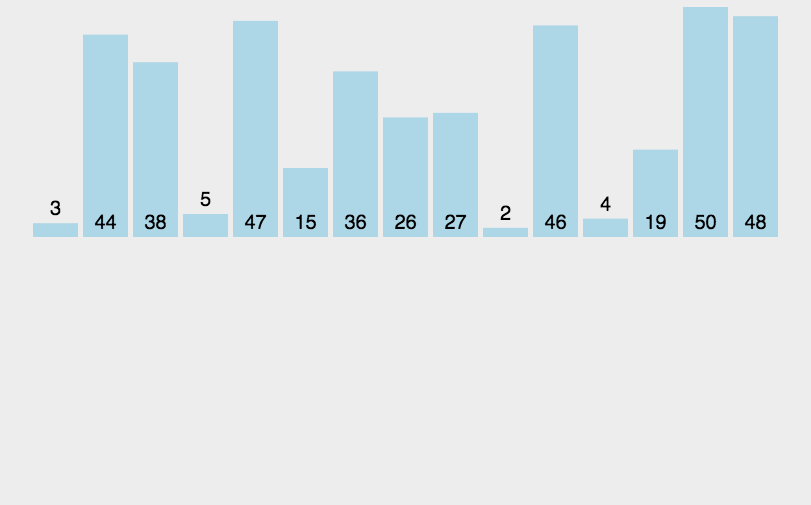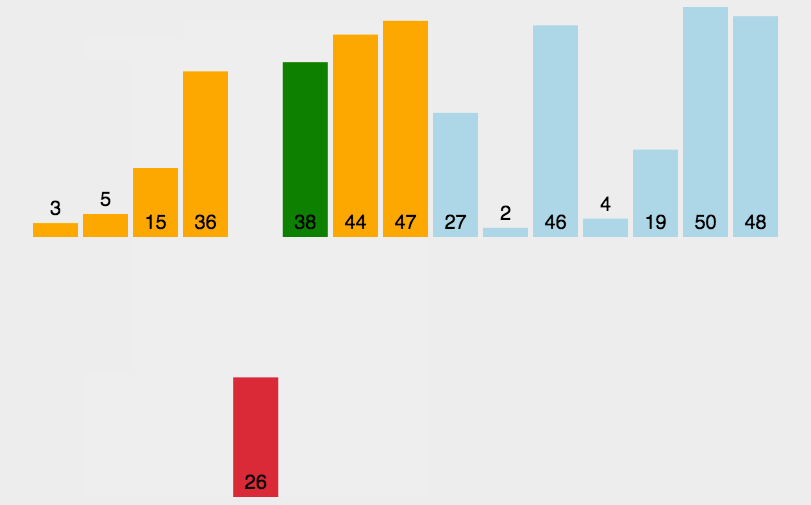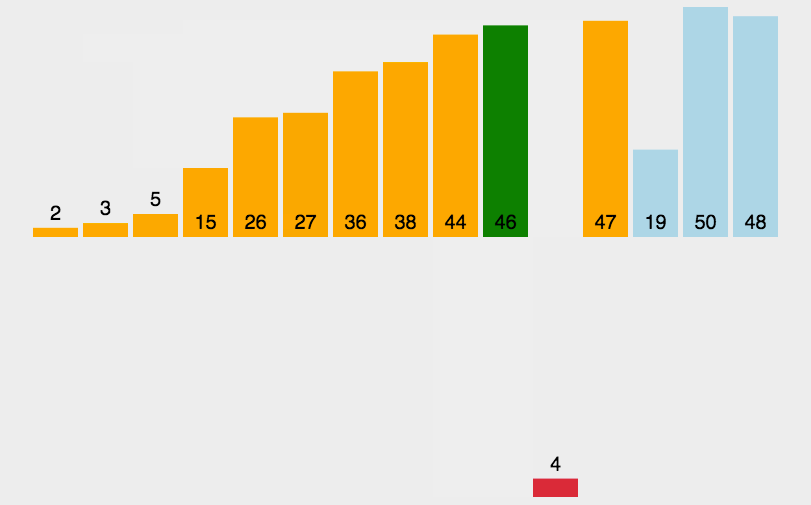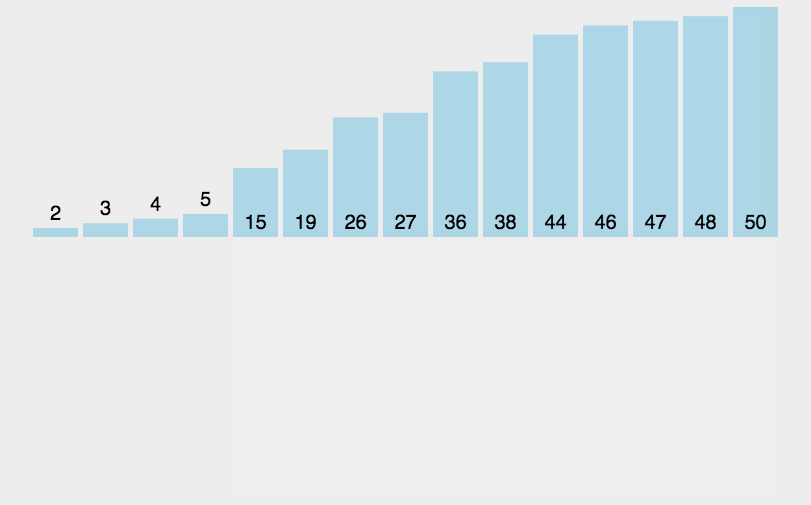
插入排序是从后往前扫描的
第一次从后到前逐个扫描下标1-0的元素,如果发现后面一个比前面小,则两个交换位置,否则就开始下一次扫描
第二次从后到前逐个扫描下标2-0的元素,如果发现后面一个比前面小,则两个交换位置 ,否则就开始下一次扫描
依此类推
- 插入排序对近乎有序的数组性能很强
for (int i = 1; i < a.length; i++) {
// 从右到左扫描,如果右值小于左值,则交换,否则跳出本轮循环
for (int j = i; j > 0; j--) {
if (less(a[j], a[j - 1])) {
swap(a, j, j - 1);
}else {
break;
}
}
}
// 改进后的插入排序
for (int i = 1; i < a.length; i++) {
var e = a[i];
int j;
for (j = i; j > 0 && greater(a[j - 1], e); j--) {
// 将
a[j]=a[j-1];
}
a[j]=e;
}
冒泡排序
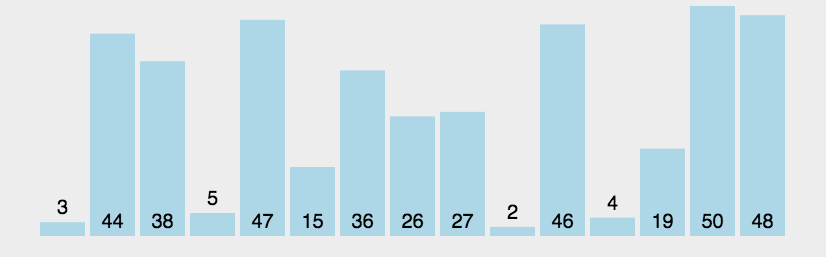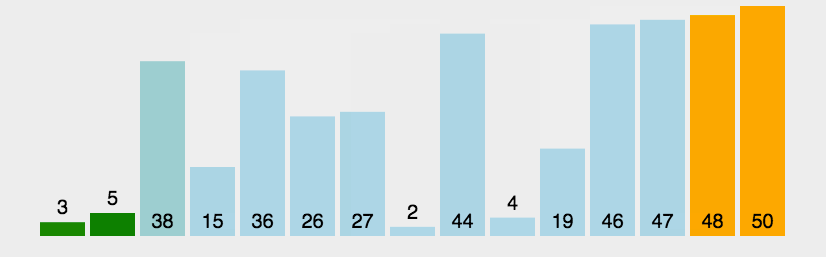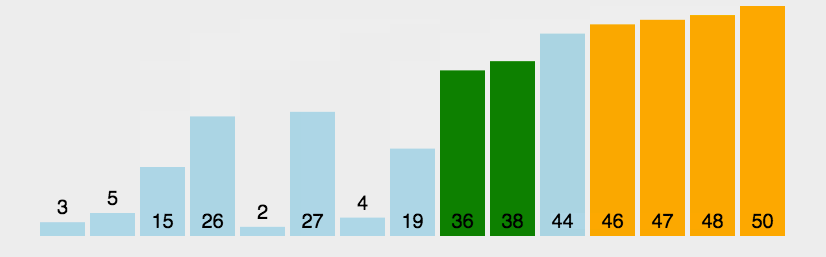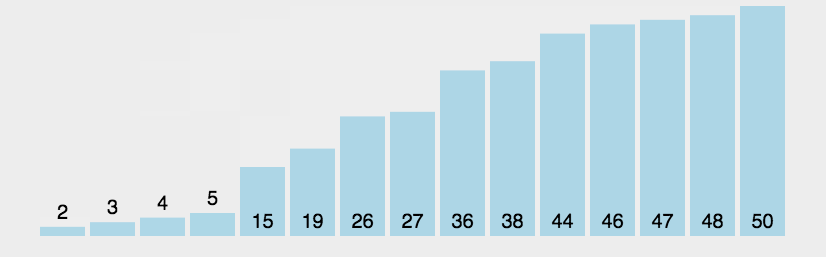
第一次扫描下标为0的元素到最后一个元素
第二次扫描下标为0的元素到倒数第二个元素
每次扫描如果发现右边比左边小 则两个交换位置
以此类推
for (int i = 1; i < a.length; i++) {
for (int j = 0; j < a.length - i; j++) {
if (less(a[i],a[j])){
swap(a,i,j);
}
}
}
// 改进的冒泡排序
for (int i = 1; i < a.length; i++) {
int lastSwap = 1;
for (int j = 0; j < a.length - i && j < lastSwap; j++) {
if (less(a[i], a[j])) {
swap(a, i, j);
// 记录最后一次交换的位置,该位置后的元素在下一轮扫描后不会被扫描
lastSwap = j;
}
}
}
希尔排序
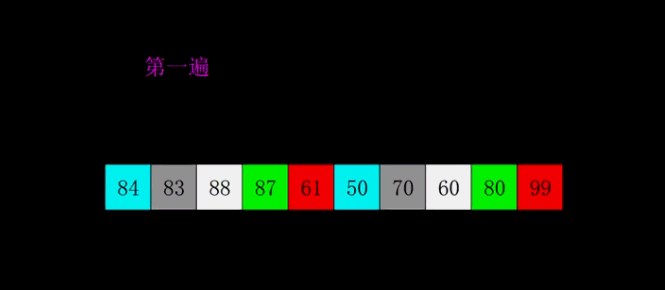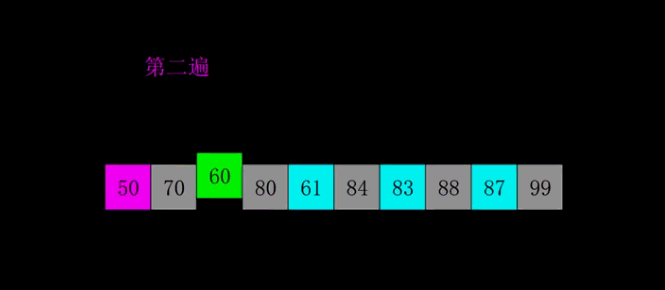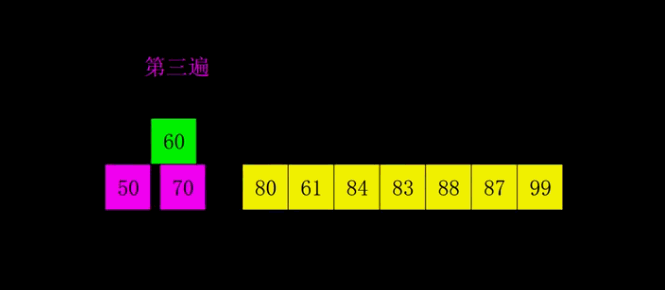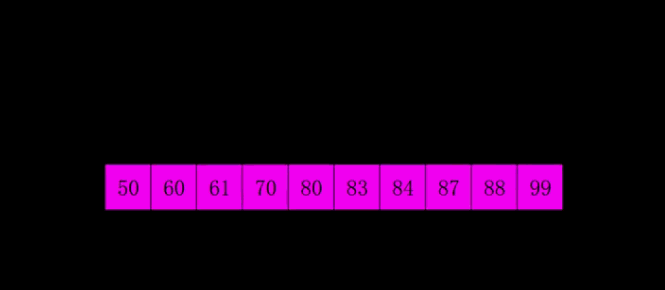
希尔排序是将插入排序中的交换相邻元素改为交换不相邻元素
- 选择一个增量序列t1,t2,…,tk
- 按增量序列个数k,对序列进行k 趟排序
int h = 1;
// 计算增长序列,1,4,13,40...
while (h < a.length / 3) {
h = 3 * h + 1;
}
while (h>=1){
for (int i = h; i < a.length; i++) {
// 对第i,i-h,i-2*h,i-3*h进行插入排序
var e = a[i];
int j;
for (j = i; j > h && less(a[j - h], e); j-=h) {
a[j]=a[j-h];
}
a[j]=e;
}
h/=3;
}
归并排序
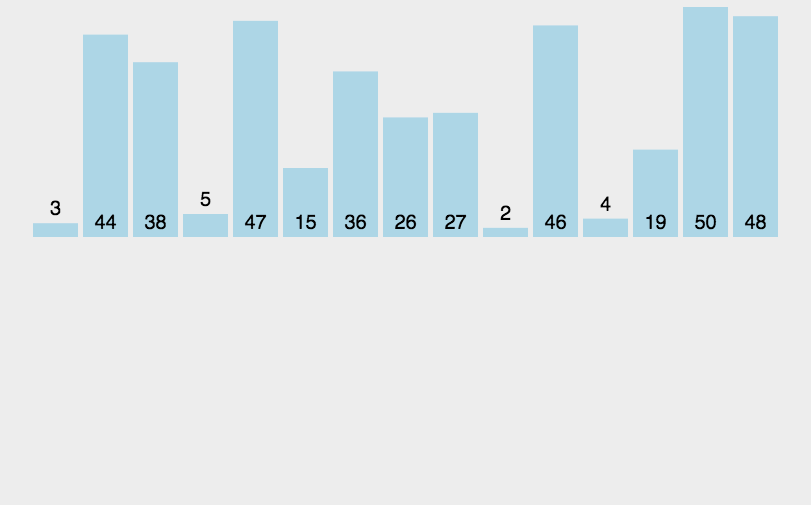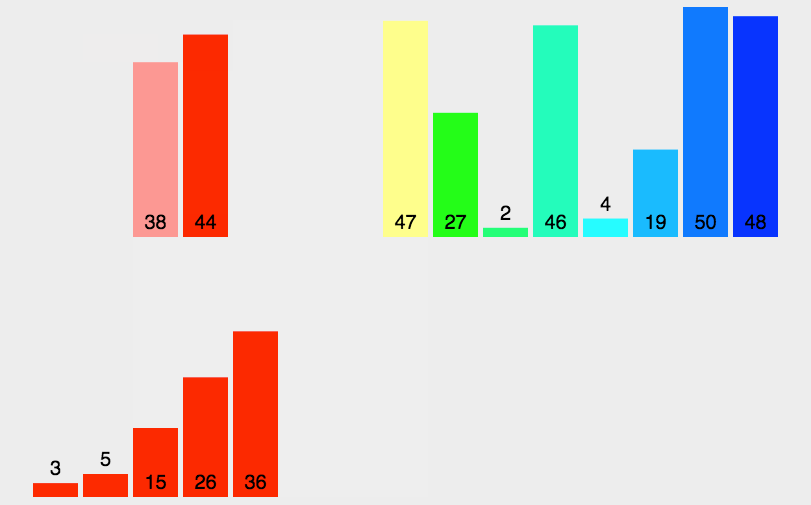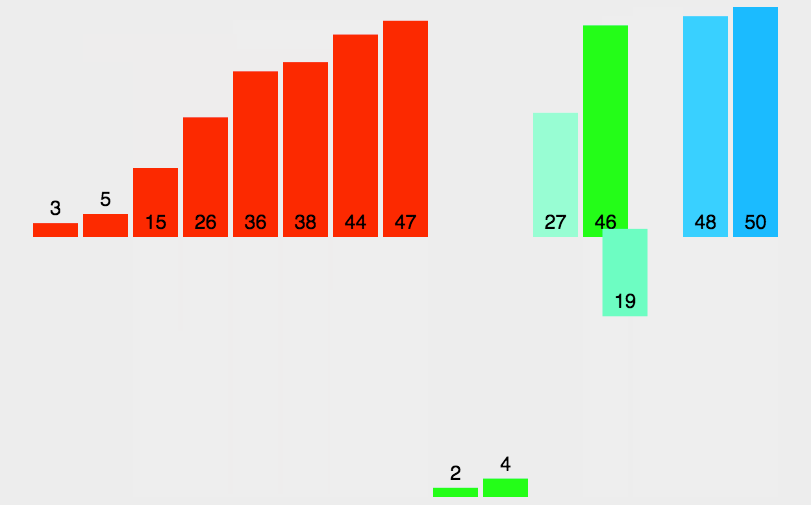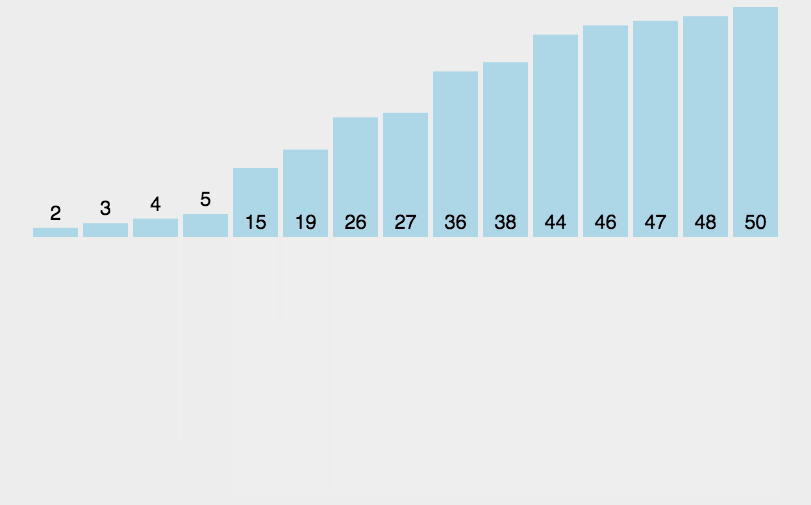
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列
对两个有序子序列进行合并,得到一个更大的有序子序列,以此类推,直到只剩下一个序列
- 但是一个缺点是需要额外的O(N)空间
private void mergeSort(Comparable<?>[] a, int l, int r) {
if (l >= r) {
return;
}
int mid = (l + r) / 2;
mergeSort(a, l, mid); // 对左边排序
mergeSort(a, mid + 1, r); // 对右边排序
merge(a, l, mid, r); // 对两个数组进行归并
}
private void merge(Comparable<?>[] a, int l, int mid, int r) {
// 开辟一块新空间给l-r之间的元素
Comparable<?>[] aux = new Comparable<?>[r - l + 1];
for (int i = l; i <= r; i++) {
aux[i - l] = a[i];
}
int i = l, j = mid + 1;
// 对l到r之间的元素进行扫描,将它们放到指定位置
for (int k = l; k <= r; k++) {
if (i > mid) { // 如果左指针已经跑过了mid,那此时让右指针去跑
a[k] = aux[j - l];
j++;
} else if (j > r) { // 如果右指针已经跑完了,则此时让左指针去跑
a[k] = aux[i - l];
i++;
} else if (less(aux[i - l], aux[j - l])) { // 否则就比较左右两指针谁的值比较小,谁小就把谁的值复制到结果里,然后该指针往后移动
a[k] = aux[i - l];
i++;
} else {
a[k] = aux[j - l];
j++;
}
}
}
优化
当mid+1位置的元素大于mid位置的元素时,就没有必要进行归并了
if (greater(a[mid],a[mid+1])){
merge(a, l, mid, r);
}
也可以当被归并排序的数组数量小于某一数量级时,使用其他排序算法,来提高性能
自底向上的归并排序
// 每次归并的数组大小依次为1 2 4 ...
for (int sz = 1; sz <= a.length; sz += sz) {
for (int i = 0; i < a.length; i += sz + sz) {
// 归并a[i...i+size-1] 与 a[i+size...i+2*size-1]
if (i + sz < a.length) { // 只有左数组长度小于整个排序数组长度使(代表目前没有右数组),才进行归并(否则数组就是有序的了)
merge(a, i, i + sz - 1, min(i + sz + sz - 1, a.length - 1));
}
}
}
外部归并排序
对于大数据量,超过内存容量的数据,归并排序可以利用外存来进行排序
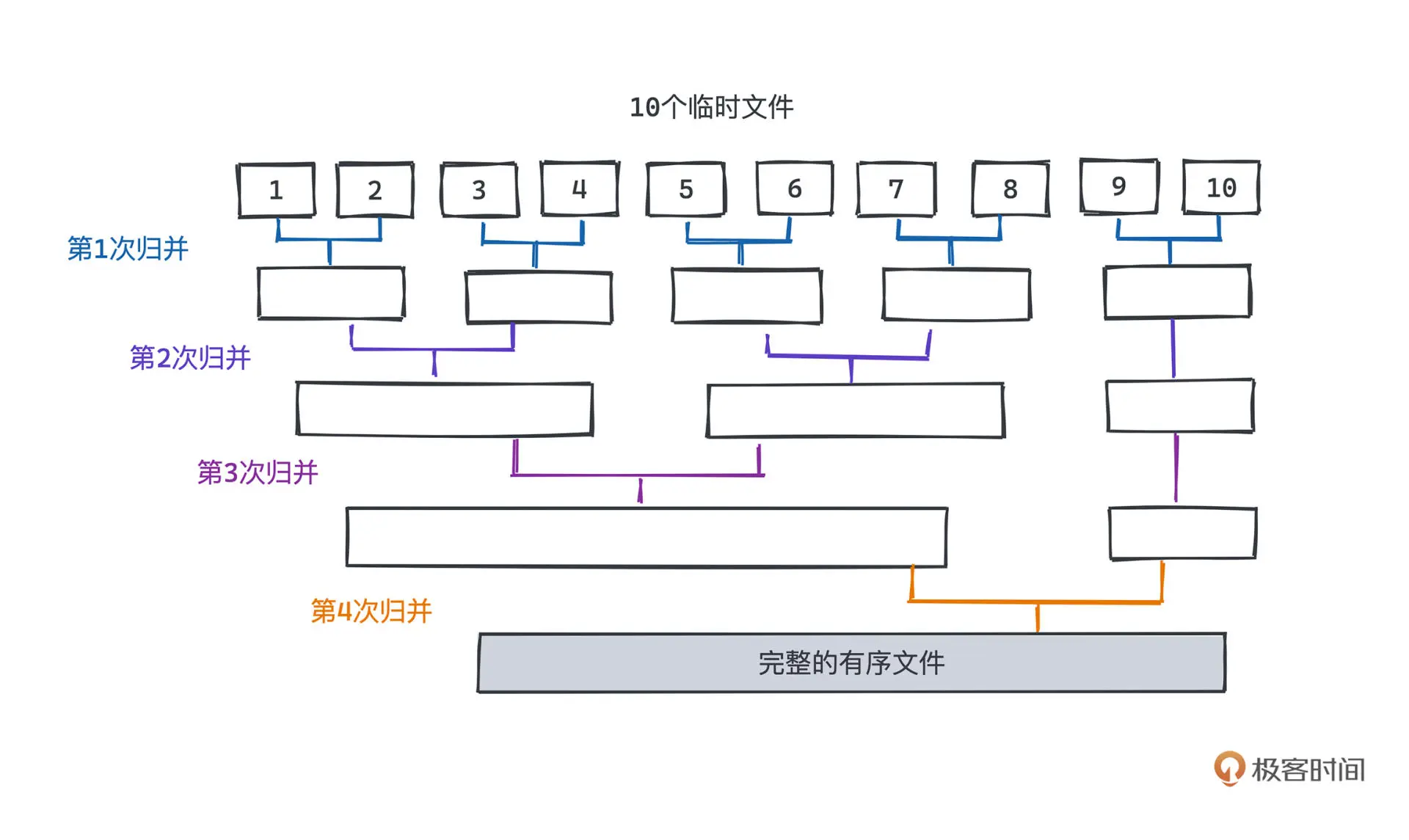
归并的层数越多,需要进行的IO次数也就越多,可以通过增加每次同时的归并文件数量,比如每次不是两辆归并,而是五五归并,减少归并层数以此来减少IO
快速排序
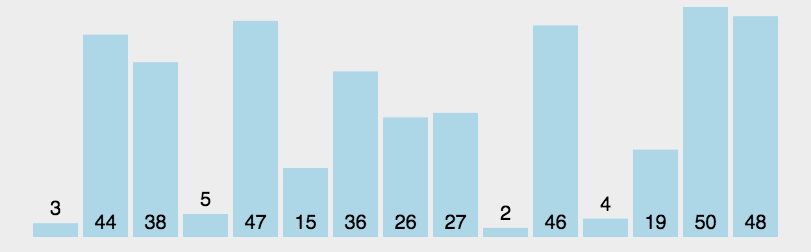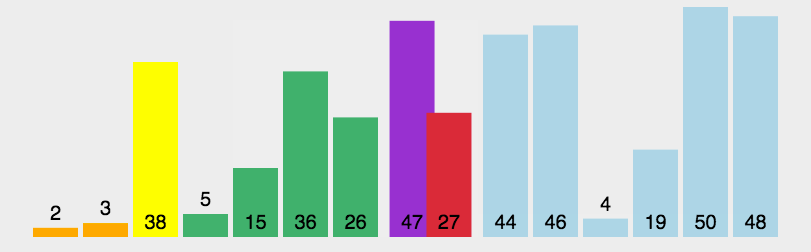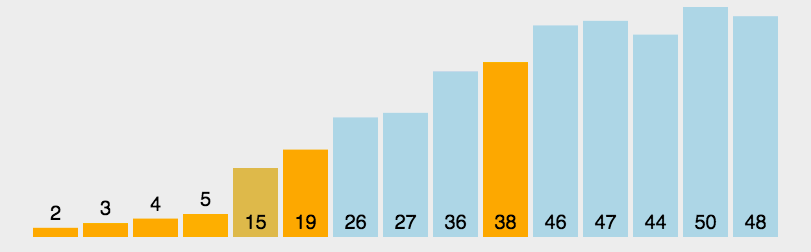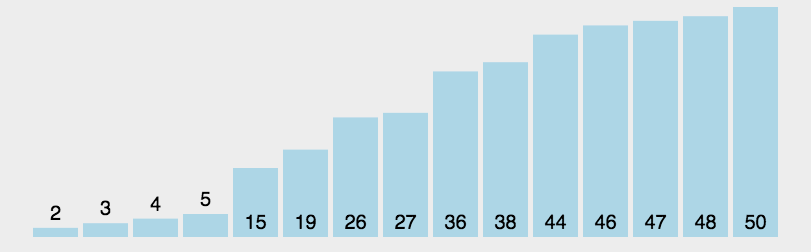
选定一个元素,将比该元素小的元素放其左边,比它大的放在其右边,并递归地对它左右两边的子序列进行排序
- 快速排序在最差的情况下,会退化为O(N^2)
private void quickSort(Comparable<?>[] a, int l, int r) {
if (l >= r) {
return;
}
int p = partition(a, l, r);
quickSort(a, l, p - 1);
quickSort(a, p + 1, r);
}
/**
* 返回一个p,使得a[l...p-1] < a[p] 并且 a[p+1...r] > a[p]
*/
private int partition(Comparable<?>[] a, int l, int r) {
var v = a[l];
int j = l;
// 从左到右扫描(一)
for (int i = l + 1; i <= r; i++) {
//如果扫描的元素小于v,则将该元素跟大数组的第一个元素交换,同时,小数组的位置扩张1(二)
if (less(a[i], v)) {
swap(a, j + 1, i);
j++;
}
}
// 最后,将v与小数组的最后一个元素交换位置(三)
swap(a, l, j);
return j;
}
一
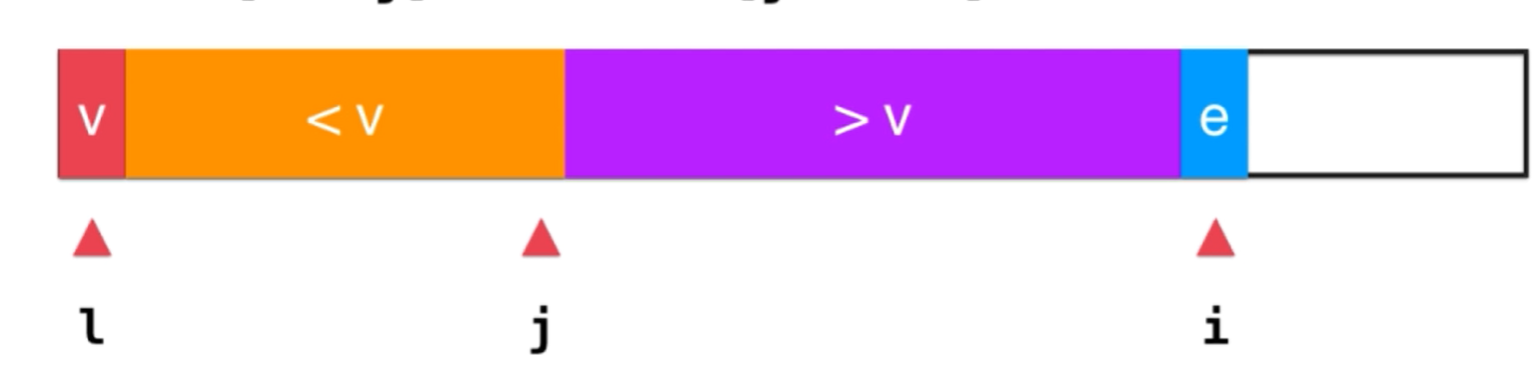
二

三
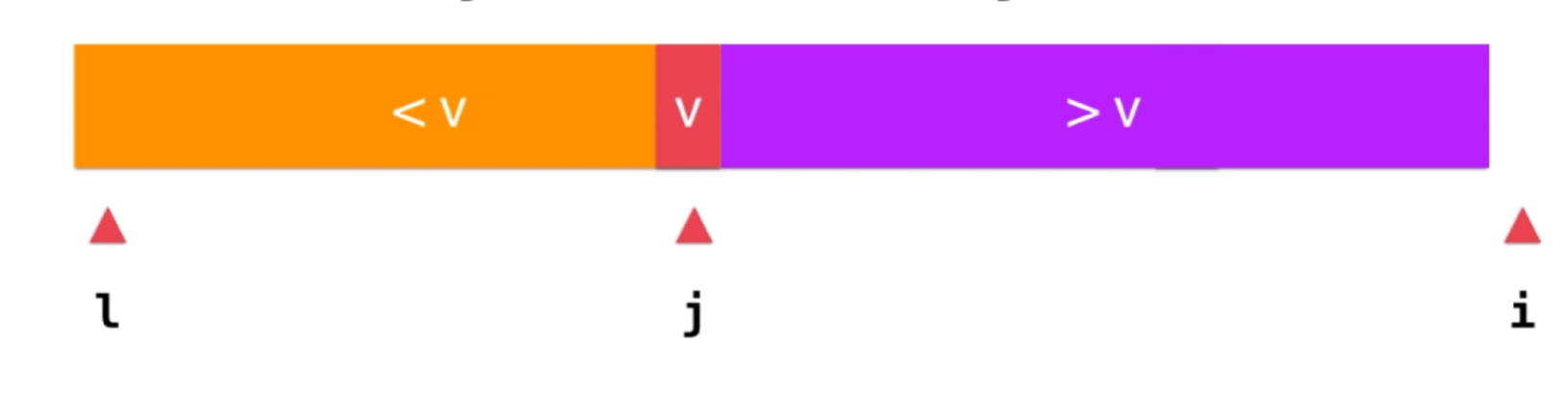
优化
当数组里有大量相同的元素,快速排序的时间复杂度为退化到N^2,解决方法是在两侧使用双指针向中间扫描
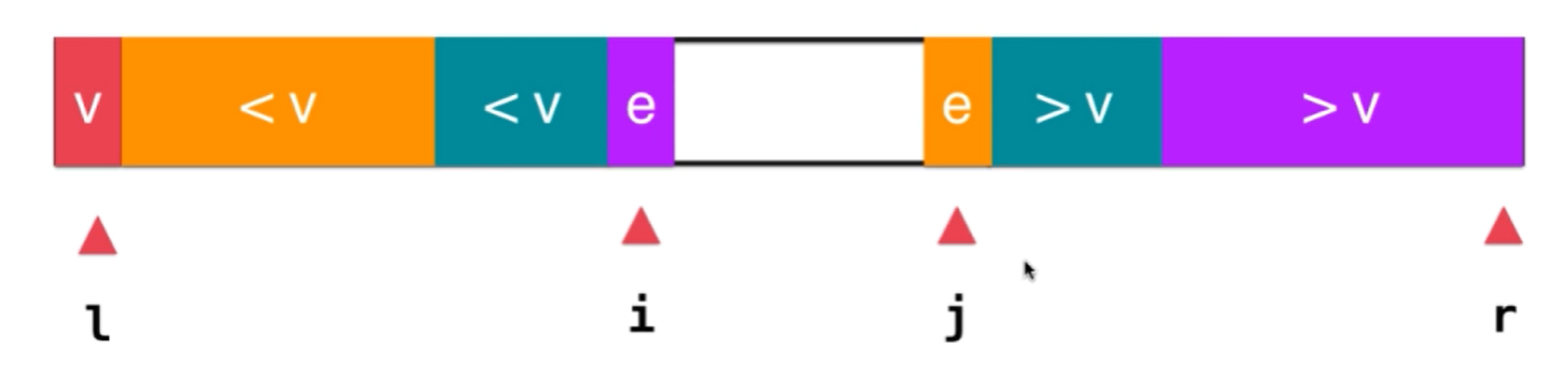
- 双路快速排序
private int partition(Comparable<?>[] a, int l, int r) {
var v = a[l];
// i:a[l+1...i] <=v j:[j...r] >=v
int i = l + 1, j = r;
while (true) {
while (i <= r && less(a[i], v)) i++;
while (j >= l + 1 && greater(a[j], v)) j--;
if (i > j) {
break;
} else {
swap(a, i, j);
i++;j--;
}
}
swap(a,l,j);
return j;
}
- 三路快速排序
private void quickSort(Comparable[] a, int l, int r) {
if (l >= r) {
return;
}
// partition
var v = a[l];
int lt = l; // a[l+1...lt] < v
int gt = r + 1; // a[gt...r] > v
int i = l + 1; // a[lt+1...i) == v
while (i < gt) {
if (a[i].compareTo(v) < 0) {
swap(a, i, lt + 1);
lt++;
i++;
} else if (a[i].compareTo(v) > 0) {
swap(a, i, gt - 1);
gt--;
}else {
i++;
}
}
swap(a,i,lt);
quickSort(a, l, lt - 1);
quickSort(a, gt, r);
}
归并排序与快速排序的背后
- 两个算法都使用了分治算法
洗牌算法
Fisher-Yates Shuffle
每次选择的时候从剩余可选的元素中随机选择一个
void Fisher_Yates_Shuffle(vector<int>& arr,vector<int>& res) {
int k;
int n = arr.size();
for (int i=0;i<n;i++) {
k=rand()%arr.size();
res.push_back(arr[k]);
arr.erase(arr.begin()+k);
}
}
- 整体的时间复杂度是 O(n^2),空间复杂度是O(n)
Knuth-Durstenfeld Shuffle
第 i 位元素和第 i~n-1 位元素中的任意一个元素交换
void shuffle(vector<int>& arr) {
for (int i = 0; i < n; i++) {
int tmp;
int target = i + rand() % (n - i);
tmp = arr[i];
arr[i] = arr[target];
arr[target] = tmp;
}
}